See the model definitions below for specifics for each model.
dreamer_data_linear(
n_cohorts,
doses,
b1,
b2,
sigma,
times,
t_max,
longitudinal = NULL,
...
)
dreamer_data_linear_binary(
n_cohorts,
doses,
b1,
b2,
link,
times,
t_max,
longitudinal = NULL,
...
)
dreamer_data_quad(
n_cohorts,
doses,
b1,
b2,
b3,
sigma,
times,
t_max,
longitudinal = NULL,
...
)
dreamer_data_quad_binary(
n_cohorts,
doses,
b1,
b2,
b3,
link,
times,
t_max,
longitudinal = NULL,
...
)
dreamer_data_loglinear(
n_cohorts,
doses,
b1,
b2,
sigma,
times,
t_max,
longitudinal = NULL,
...
)
dreamer_data_loglinear_binary(
n_cohorts,
doses,
b1,
b2,
link,
times,
t_max,
longitudinal = NULL,
...
)
dreamer_data_logquad(
n_cohorts,
doses,
b1,
b2,
b3,
sigma,
times,
t_max,
longitudinal = NULL,
...
)
dreamer_data_logquad_binary(
n_cohorts,
doses,
b1,
b2,
b3,
link,
times,
t_max,
longitudinal = NULL,
...
)
dreamer_data_emax(
n_cohorts,
doses,
b1,
b2,
b3,
b4,
sigma,
times,
t_max,
longitudinal = NULL,
...
)
dreamer_data_emax_binary(
n_cohorts,
doses,
b1,
b2,
b3,
b4,
link,
times,
t_max,
longitudinal = NULL,
...
)
dreamer_data_exp(
n_cohorts,
doses,
b1,
b2,
b3,
sigma,
times,
t_max,
longitudinal = NULL,
...
)
dreamer_data_exp_binary(
n_cohorts,
doses,
b1,
b2,
b3,
link,
times,
t_max,
longitudinal = NULL,
...
)
dreamer_data_beta(
n_cohorts,
doses,
b1,
b2,
b3,
b4,
scale,
sigma,
times,
t_max,
longitudinal = NULL,
...
)
dreamer_data_beta_binary(
n_cohorts,
doses,
b1,
b2,
b3,
b4,
scale,
link,
times,
t_max,
longitudinal = NULL,
...
)
dreamer_data_independent(
n_cohorts,
doses,
b1,
sigma,
times,
t_max,
longitudinal = NULL,
...
)
dreamer_data_independent_binary(
n_cohorts,
doses,
b1,
link,
times,
t_max,
longitudinal = NULL,
...
)Arguments
- n_cohorts
a vector listing the size of each cohort.
- doses
a vector listing the dose for each cohort.
- b1, b2, b3, b4
parameters in the models. See sections below for each parameter's interpretation in a given model.
- sigma
standard deviation.
- times
the times at which data should be simulated if a longitudinal model is specified.
- t_max
the t_max parameter used in the longitudinal model.
- longitudinal
a string indicating the longitudinal model to be used. Can be "linear", "itp", or "idp".
- ...
additional longitudinal parameters.
- link
character vector indicating the link function for binary models.
- scale
a scaling parameter (fixed, specified by the user) for the beta models.
Value
A dataframe of random subjects from the specified model and parameters.
Functions
dreamer_data_linear(): generate data from linear dose response.dreamer_data_linear_binary(): generate data from linear binary dose response.dreamer_data_quad(): generate data from quadratic dose response.dreamer_data_quad_binary(): generate data from quadratic binary dose response.dreamer_data_loglinear(): generate data from log-linear dose response.dreamer_data_loglinear_binary(): generate data from binary log-linear dose response.dreamer_data_logquad(): generate data from log-quadratic dose response.dreamer_data_logquad_binary(): generate data from log-quadratic binary dose response.dreamer_data_emax(): generate data from EMAX dose response.dreamer_data_emax_binary(): generate data from EMAX binary dose response.dreamer_data_exp(): generate data from exponential dose response.dreamer_data_exp_binary(): generate data from exponential binary dose response.dreamer_data_beta(): generate data from Beta dose response.dreamer_data_beta_binary(): generate data from binary Beta dose response.dreamer_data_independent(): generate data from an independent dose response.dreamer_data_independent_binary(): generate data from an independent dose response.
Linear
$$y \sim N(f(d), \sigma^2)$$ $$f(d) = b_1 + b_2 * d$$ $$b_1 \sim N(mu_b1, sigma_b1 ^ 2)$$ $$b_2 \sim N(mu_b2, sigma_b2 ^ 2)$$ $$1 / \sigma^2 \sim Gamma(shape, rate)$$
Quadratic
$$y \sim N(f(d), \sigma^2)$$ $$f(d) = b_1 + b_2 * d + b_3 * d^2$$ $$b_1 \sim N(mu_b1, sigma_b1 ^ 2)$$ $$b_2 \sim N(mu_b2, sigma_b2 ^ 2)$$ $$b_3 \sim N(mu_b3, sigma_b3 ^ 2)$$ $$1 / \sigma^2 \sim Gamma(shape, rate)$$
Log-linear
$$y \sim N(f(d), \sigma^2)$$ $$f(d) = b_1 + b_2 * log(d + 1)$$ $$b_1 \sim N(mu_b1, sigma_b1 ^ 2)$$ $$b_2 \sim N(mu_b2, sigma_b2 ^ 2)$$ $$1 / \sigma^2 \sim Gamma(shape, rate)$$
Log-quadratic
$$y \sim N(f(d), \sigma^2)$$ $$f(d) = b_1 + b_2 * log(d + 1) + b_3 * log(d + 1)^2$$ $$b_1 \sim N(mu_b1, sigma_b1 ^ 2)$$ $$b_2 \sim N(mu_b2, sigma_b2 ^ 2)$$ $$b_3 \sim N(mu_b3, sigma_b3 ^ 2)$$ $$1 / \sigma^2 \sim Gamma(shape, rate)$$
EMAX
$$y \sim N(f(d), \sigma^2)$$ $$f(d) = b_1 + (b_2 - b_1) * d ^ b_4 / (exp(b_3 * b_4) + d ^ b_4)$$ $$b_1 \sim N(mu_b1, sigma_b1 ^ 2)$$ $$b_2 \sim N(mu_b2, sigma_b2 ^ 2)$$ $$b_3 \sim N(mu_b3, sigma_b3 ^ 2)$$ $$b_4 \sim N(mu_b4, sigma_b4 ^ 2), (Truncated above 0)$$ $$1 / \sigma^2 \sim Gamma(shape, rate)$$ Here, \(b_1\) is the placebo effect (dose = 0), \(b_2\) is the maximum treatment effect, \(b_3\) is the \(log(ED50)\), and \(b_4\) is the hill or rate parameter.
Exponential
$$y \sim N(f(d), \sigma^2)$$ $$f(d) = b_1 + b_2 * (1 - exp(- b_3 * d))$$ $$b_1 \sim N(mu_b1, sigma_b1 ^ 2)$$ $$b_2 \sim N(mu_b2, sigma_b2 ^ 2)$$ $$b_3 \sim N(mu_b3, sigma_b3 ^ 2), (truncated to be positive)$$ $$1 / \sigma^2 \sim Gamma(shape, rate)$$
Linear Binary
$$y \sim Binomial(n, f(d))$$ $$link(f(d)) = b_1 + b_2 * d$$ $$b_1 \sim N(mu_b1, sigma_b1 ^ 2)$$ $$b_2 \sim N(mu_b2, sigma_b2 ^ 2)$$
Quadratic Binary
$$y \sim Binomial(n, f(d))$$ $$link(f(d)) = b_1 + b_2 * d + b_3 * d^2$$ $$b_1 \sim N(mu_b1, sigma_b1 ^ 2)$$ $$b_2 \sim N(mu_b2, sigma_b2 ^ 2)$$ $$b_3 \sim N(mu_b3, sigma_b3 ^ 2)$$
Log-linear Binary
$$y \sim Binomial(n, f(d))$$ $$link(f(d)) = b_1 + b_2 * log(d + 1)$$ $$b_1 \sim N(mu_b1, sigma_b1 ^ 2)$$ $$b_2 \sim N(mu_b2, sigma_b2 ^ 2)$$
Log-quadratic Binary
$$y \sim Binomial(n, f(d))$$ $$link(f(d)) = b_1 + b_2 * log(d + 1) + b_3 * log(d + 1)^2$$ $$b_1 \sim N(mu_b1, sigma_b1 ^ 2)$$ $$b_2 \sim N(mu_b2, sigma_b2 ^ 2)$$ $$b_3 \sim N(mu_b3, sigma_b3 ^ 2)$$
EMAX Binary
$$y \sim Binomial(n, f(d))$$ $$link(f(d)) = b_1 + (b_2 - b_1) * d ^ b_4 / (exp(b_3 * b_4) + d ^ b_4)$$ $$b_1 \sim N(mu_b1, sigma_b1 ^ 2)$$ $$b_2 \sim N(mu_b2, sigma_b2 ^ 2)$$ $$b_3 \sim N(mu_b3, sigma_b3 ^ 2)$$ $$b_4 \sim N(mu_b4, sigma_b4 ^ 2), (Truncated above 0)$$ Here, on the \(link(f(d))\) scale, \(b_1\) is the placebo effect (dose = 0), \(b_2\) is the maximum treatment effect, \(b_3\) is the \(log(ED50)\), and \(b_4\) is the hill or rate parameter.
Exponential Binary
$$y \sim Binomial(n, f(d))$$ $$link(f(d)) = b_1 + b_2 * (exp(b_3 * d) - 1)$$ $$b_1 \sim N(mu_b1, sigma_b1 ^ 2)$$ $$b_2 \sim N(mu_b2, sigma_b2 ^ 2)$$ $$b_3 \sim N(mu_b3, sigma_b3 ^ 2), (Truncated below 0)$$
Independent
$$y \sim N(f(d), \sigma^2)$$ $$f(d) = b_{1d}$$ $$b_{1d} \sim N(mu_b1[d], sigma_b1[d] ^ 2)$$ $$1 / \sigma^2 \sim Gamma(shape, rate)$$
Independent Binary
$$y \sim Binomial(n, f(d))$$ $$link(f(d)) = b_{1d}$$ $$b_{1d} \sim N(mu_b1[d], sigma_b1[d]) ^ 2$$
Longitudinal Linear
Let \(f(d)\) be a dose response model. The expected value of the response, y, is: $$E(y) = g(d, t)$$ $$g(d, t) = a + (t / t_max) * f(d)$$ $$a \sim N(mu_a, sigma_a)$$
Longitudinal ITP
Let \(f(d)\) be a dose response model. The expected value of the response, y, is: $$E(y) = g(d, t)$$ $$g(d, t) = a + f(d) * ((1 - exp(- c1 * t))/(1 - exp(- c1 * t_max)))$$ $$a \sim N(mu_a, sigma_a)$$ $$c1 \sim Uniform(a_c1, b_c1)$$
Longitudinal IDP
Increasing-Decreasing-Plateau (IDP).
Let \(f(d)\) be a dose response model. The expected value of the response, y, is: $$E(y) = g(d, t)$$ $$g(d, t) = a + f(d) * (((1 - exp(- c1 * t))/(1 - exp(- c1 * d1))) * I(t < d1) + (1 - gam * ((1 - exp(- c2 * (t - d1))) / (1 - exp(- c2 * (d2 - d1))))) * I(d1 <= t <= d2) + (1 - gam) * I(t > d2))$$ $$a \sim N(mu_a, sigma_a)$$ $$c1 \sim Uniform(a_c1, b_c1)$$ $$c2 \sim Uniform(a_c2, b_c2)$$ $$d1 \sim Uniform(0, t_max)$$ $$d2 \sim Uniform(d1, t_max)$$ $$gam \sim Uniform(0, 1)$$
Examples
set.seed(888)
data <- dreamer_data_linear(
n_cohorts = c(20, 20, 20),
dose = c(0, 3, 10),
b1 = 1,
b2 = 3,
sigma = 5
)
head(data)
#> cohort dose subject response
#> 1 1 0 1 -8.7567167
#> 2 1 0 2 -6.7218308
#> 3 1 0 3 4.6491635
#> 4 1 0 4 -0.3879090
#> 5 1 0 5 -7.2814217
#> 6 1 0 6 -0.2551169
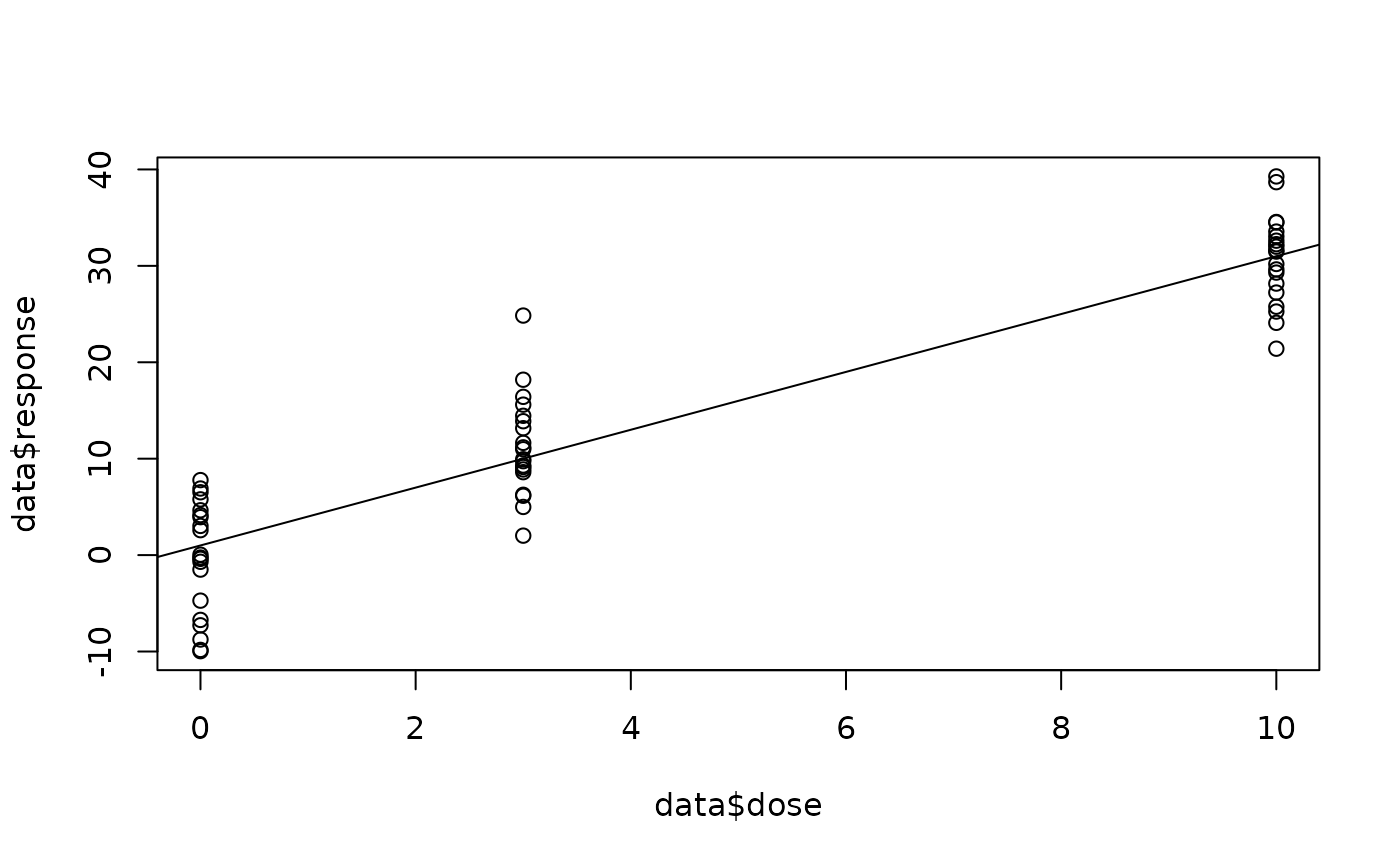
plot(data$dose, data$response)
abline(a = 1, b = 3)
# longitudinal data
set.seed(889)
data_long <- dreamer_data_linear(
n_cohorts = c(10, 10, 10, 10), # number of subjects in each cohort
doses = c(.25, .5, .75, 1.5), # dose administered to each cohort
b1 = 0, # intercept
b2 = 2, # slope
sigma = .5, # standard deviation,
longitudinal = "itp",
times = c(0, 12, 24, 52),
t_max = 52, # maximum time
a = .5,
c1 = .1
)
if (FALSE) { # \dontrun{
ggplot(data_long, aes(time, response, group = dose, color = factor(dose))) +
geom_point()
} # }